A organização coletiva é uma estratégia de sobrevivência observada em muitas espécies, das formas de vida microscópicas até alguns dos maiores animais conhecidos. Mas indivíduos solitários – aqueles deslocados, que não seguem as tendências do grupo – são quase tão comuns quanto, e, de acordo com um estudo publicado no último mês de março no periódico Plos Biology, os solitários podem servir também a um propósito crucial para a conservação da espécie. A descoberta foi possível graças a experimentos realizados com a ameba Dictyostelium discoideum na Universidade de Princeton, em Nova Jersey, Estados Unidos, por uma equipe multidisciplinar e internacional que contou com o pesquisador Ricardo Martinez-Garcia, professor  SIMONS-FAPESP no ICTP-SAIFR e no Instituto de Física Teórica da UNESP, em São Paulo.

Corpo multicelular da ameba Dictyostelium discoideum. Indivíduos unicelulares se agregam para formar uma estrutura de caule e esporos como estratégia de sobrevivência. Foto: Tyler Larsen/Creative Commons.

Desde os movimentos de migração coletiva feitos por algumas espécies de aves ou mamíferos, até o florescimento sincronizado de certas plantas, ecólogos sempre observaram a existência de certos indivíduos de um grupo que parecem se recusar a seguir o mesmo comportamento da maioria. Do ponto de vista biológico, estes solitários sempre foram encarados como pontos fora da curva, isto é, casos de comportamento anômalo, erros na tentativa de coordenar uma ação coletiva complexa. No entanto, o artigo publicado na edição de 19 de março no periódico Plos Biology sugere que tal comportamento pode também fazer parte de uma estratégia biológica de sobrevivência e promoção de diversidade.

A vida da ameba D. discoideum possui duas fases, marcadas por uma manobra de sobrevivência peculiar: enquanto as amebas estiverem inseridas em um meio com disponibilidade de alimento, vivem como organismos unicelulares individuais, porém, ao encararem a escassez, as amebas iniciam um movimento auto-organizado de agregação, formando um organismo multicelular em formato de um caule com uma aglutinação de amebas em forma de esporos na sua ponta. As células que formam o caule acabam morrendo, mas aquelas no topo possuem maior chance de acabar entrando em contato com insetos ou animais passageiros e assim serem transportadas para um novo local, com maior quantidade de alimentos disponíveis. Muitos estudos têm focado no entendimento da transição de fases do ciclo de vida dessa ameba, mas pouca atenção havia sido dada até então às células solitárias.

Um dos autores do trabalho, o Dr. Ricardo Martinez-Garcia dedica-se à área da física aplicada à biologia, buscando entender sistemas ecológicos do ponto de vista da física estatística: “Não procuramos o comportamento individual de cada uma das células, plantas ou animais, mas o que realmente tratamos de descrever com precisão são as interações [entre as componentes do sistema e, a partir delas entender como surgem os padrões que observamos na escala macroscópica.”, explica o professor em entrevista concedida por videoconferência. No caso da D. discoideum, Martinez-Garcia e seus colaboradores usaram essa abordagem para descrever o mecanismo de transição entre as fases unicelular e multicelular, e assim foram capazes de criar um modelo que leva em conta inclusive as amebas solitárias que não se envolvem no processo de transição.

Ricardo Martinez-Garcia é professor SIMONS FAPESP no ICTP-SAIFR e no IFT-UNESP. O trabalho “Eco-evolutionary significance of ‘loners’” foi desenvolvido em parceria com colaboradores da Universidade de Princeton, onde realizou seu pós-doutorado. Os co-autores da pesquisa foram Fernando W. Rossine (Universidade de Princeton, Estados Unidos), Allyson E. Sgro (Universidade de Princeton e Universidade de Boston, Estados Unidos), Thomas Gregor (Universidade de Princeton, Estados Unidos e Instituto Pasteur, França) e Corina E. Tarnita (Universidade de Princeton, Estados Unidos). Foto cedida por Ricardo Martinez-Garcia.

Quando perguntado sobre o funcionamento deste modelo, o Prof. Martinez-Garcia explica que nesse processo de transição, a comunicação entre as células se dá por sinais bioquímicos: uma vez que o alimento do ambiente começa a se esgotar, a célula passa a secretar substâncias que, quando detectadas pelas suas vizinhas, podem provocar o início do processo de agregação. “A nossa hipótese para a origem dessas amebas solitárias é uma resposta tardia, que ocorre por algum motivo que não identificamos molecularmente. Quando elas vão responder ao sinal, já não há mais uma massa crítica [nas suas vizinhanças]. A agregação precisa de um número de células grande, com duas ou três não tem início o comportamento coletivo. (…) Como há uma falta de sincronia na resposta, as que responderem mais tarde, de certa maneira, chegarão atrasadas para o comportamento coletivo”. Baseando-se nisso, construíram um modelo matemático que leva em consideração duas escalas de tempo: o tempo que todo o processo de agregação leva para ser completado, e o tempo que uma célula pode levar para responder ao sinal bioquímico. Se o tempo de resposta de uma célula é maior do que o tempo médio no qual todo o resto da população se agrega, a célula sobra como um indivíduo solitário.

Isso mostra que os indivíduos solitários, ao menos no caso da ameba D. discoideum, não são simples resultado de um processo aleatório ou fora do controle do próprio organismo – pelo contrário, eles surgem pelo próprio processo coletivo de auto-organização. E isso significa que a seleção natural poderia estar escolhendo esse comportamento, isto é, o comportamento solitário pode ser uma característica passada adiante no processo de reprodução, com possíveis consequências ecológicas. “É uma mudança radical na maneira como se estuda comportamentos coletivos na natureza. Ao menos nessas amebas, temos evidência experimental de que os indivíduos solitários não são erros. Eles certamente estão regulados pelo organismo, e poderiam ter um papel muito importante na ecologia e na evolução da espécie. Essa é a maior mensagem.”

O professor continua explicando que, por não estarem tão envolvidos no comportamento social, um dos papéis fundamentais que os solitários podem estar desempenhando é que, caso os esforços coletivos não sejam suficientes para a sobrevivência da população, ou caso esta seja destruída no processo por algum agente externo, aqueles que não participaram da mobilização do grupo serão sobreviventes com a capacidade de reconstruir e dar continuidade à espécie. “Por exemplo, o bambu tem um período de florescimento que é muito fechado – numa parte muito específica do ano – mas que também não é perfeito. Alguns produzem as flores mais tarde ou mais cedo que o resto da população. Nisso temos uma conexão muito mais clara de se fazer: imagine que todas as flores crescem no mesmo dia, se neste dia fizer um sol muito forte, nevar ou qualquer coisa assim, toda a população vai morrer. Mas se você tem esses indivíduos não sociais que por alguma razão produzem as flores um mês antes ou depois, você de certa maneira tem uma distribuição do risco.”

Os mecanismos por trás do surgimento de solitários certamente diferem ao se olhar para sistemas de espécies diferentes. Enquanto o modelo criado neste trabalho é capaz de descrever o processo para a D. discoideum, com direito a evidências experimentais, em outros reinos da vida natural os mecanismos por trás disso continuam desconhecidos. “Infelizmente trabalhar com pessoas ou com animais maiores é muito mais complicado. Mesmo com a ameba a experimentação foi extremamente complexa.”, explica. “Nós procuramos muitos exemplos na natureza. Tem, por exemplo, os gnus: eles fazem migrações muito grandes, nas quais a população coordena entre si para se mudarem todos juntos. Mas quando ecólogos seguem essas populações, veem que alguns animais ficam para trás ou não tomam parte da migração coletiva. Outro exemplo são gafanhotos: quando você tem muitos gafanhotos juntos há uma mudança de comportamento, eles transicionam de solitários para sociais. Mas se você observa por muito tempo um grupo muito grande deles, nem todos fazem essa transição.”

“Mesmo na população de humanos temos os ‘do contra’: são pessoas que vão contra opiniões gerais. Se você quiser extrapolar, podemos ficar no contexto da formação de opinião e tendências sociais. [Mas] acho que isso é muito mais hipotético. (…) Nós sabemos que no mundo natural temos exemplos mais claros.” Com uma última ressalva, o professor ainda faz uma breve consideração sobre a pandemia do vírus Sars-Cov-2: “Temos um caso muito claro com a pandemia. A não-socialidade agora é muito importante para preservar a sociedade, se quisermos olhar assim. Mas a extrapolação para humanos fica totalmente fora do objetivo do estudo.” Mesmo não sendo completamente extrapolável para outras espécies de seres vivos, os resultados que o Prof. Martinez-Garcia e seus colaboradores apresentam neste trabalho implicam numa nova maneira de se olhar para a ecologia. Além disso, é um grande passo inicial que incentiva a pesquisa com grupos de seres vivos cada vez mais complexos, como insetos, plantas e vertebrados. Agora se entende melhor o que são esses indivíduos solitários, antes considerados erros aleatórios da natureza. “É o que se falava antes: ‘eles estão aí, mas não são importantes’. Agora a pergunta mudou: na verdade eles fazem parte do comportamento coletivo, então que papel eles desempenham de um ponto de vista ecológico e evolutivo?”.

O que a evolução de espécies, as rotas de transporte de mercadorias e a eleição democrática de representantes têm em comum? Do ponto de vista da física (e da matemática), tudo!

O último Papos de Física de 2019 aconteceu no dia 7 de novembro e, para fechar o ano, abordamos uma temática inusitada: Sistemas Complexos e o olhar da Física. Sistemas complexos formam uma área de estudo relativamente nova, naturalmente interdisciplinar, que tem reunido físicos, matemáticos, biólogos, sociólogos e até mesmo economistas, para resolver questões em comum. O professor Daniel Stariolo, da Universidade Federal Fluminense (UFF), foi ao Tubaína Bar falar um pouco sobre o assunto e a perspectiva da física dentro desta área.

O professor Daniel Stariolo conversou sobre Sistemas Complexos e como a física ajuda a entendê-los.

Stariolo começou a apresentação ilustrando a natureza interdisciplinar dos sistemas complexos e sua ocorrência nas mais diversas áreas de ciências e fora dela, desde os ecossistemas do planeta, planejamento de transporte e estradas, organizações sociais, evolução… O ponto em comum entre todos eles é o fato de funcionarem em redes e serem, de alguma forma, internamente conectados entre si. Os sistemas complexos podem ser naturais, que evoluíram para serem da forma como são hoje (como os ecossistemas, os organismos, o clima) ou podem ser artificiais, criados pelo homem para funcionarem do modo que conhecemos atualmente (a economia, as redes de distribuição de energia, o sistema de transporte e as redes sociais).

Alguns elementos são essenciais e caracterizam os sistemas complexos. Os principais são a existência de muitos agentes, a conectividade (relação entre os agentes) e a existência de vínculos conflitantes (ou seja, relações competitivas). Porém, não basta que esses elementos existam. Algumas propriedades do sistema surgem como consequência das características individuais dos agentes: são as chamadas propriedades emergentes.

As interações entre as partes de um sistema complexo criam padrões complexos de funcionamento coletivo. Em outras palavras, propriedades emergentes são criadas por conta da interação entre os agentes do sistemas, mas não estão presentes individualmente em cada uma das partes. Por exemplo, a interação entre os neurônios no seu cérebro permitem que você leia e entenda esse texto. Porém, um único neurônio não seria capaz de realizar a mesma atividade. Uma pessoa levantar e abaixar os braços não implica em nada; porém milhares de pessoas fazendo isso (organizadamente) nas arquibancadas de um estádio cria uma “ola”.

via GIPHY

Dentre as inúmeras propriedades emergentes de um sistema complexo, Stariolo destacou auto organização, múltiplas escalas e complexidade.

A auto organização é inerente ao sistema e é o conjunto de regras internas que faz ele funcionar. Essa rede de relações e regras gera um fluxo de informações entre os indivíduos do sistema e, em geral, é bastante complexa para entender, e, principalmente, modelar. Quando inserido em um sistema, o indivíduo fica sujeito a essas leis de funcionamento. Por exemplo, quando começamos num trabalho novo, temos que entender (e nos adequar) a dinâmica do ambiente e suas regras, sejam elas de comportamento ou vestimenta; quando viajamos a países estrangeiros, devemos atender às leis daquele lugar e estamos sujeitos à sua constituição (via de regra… Em geral, Direito é bem mais complexo do que isso!).

As múltiplas escalas também são muito presentes nos sistemas complexos. Os próprios sistemas em geral são compostos de subsistemas, mas podem interagir com outros sistemas maiores, gerando redes de relação em escalas diferentes. Embora cada escala tenha suas regras próprias, elas se relacionam umas com as outras e também podem interferir umas nas outras.

Para entender as escalas diferentes, imagine seu corpo. Ele é formado por órgãos – pulmão, coração, rins, etc. Alguns órgãos atuam juntos e formam sistemas – respiratório, digestório, cardiovascular – e todos eles juntos formam você, que é também um sistema complexo. Se diminuirmos a escala, cada órgão é formado por tecidos diferentes – muscular, nervoso, epitelial – e cada tecido é formado por tipos específicos de célula. Ou seja, a medida que aumentamos ou diminuímos a escala, observam-se padrões e a ocorrência de sistemas complexos, com organização e regras próprios, mas que interferem uns nos outros.

O conceito de Complexidade é estudado e utilizado em diversas áreas de conhecimento, em ciências humanas, da vida e exatas, e a própria definição é controversa. No Papos de Física, Stariolo definiu a complexidade dos sistemas complexos pela possibilidade de existirem múltiplos equilíbrios possíveis para o sistema em questão. E usou a evolução de espécies para ilustrar isso. 

A evolução a partir da seleção natural envolve inúmeros indivíduos (são 8,7 milhões de formas de vida hoje, sem considerar as já extintas!), explora as relações entre eles (sejam harmônicas ou desarmônicas, onde nenhuma ou alguma das partes sai prejudicada) e certamente apresenta vínculos conflitantes (sobrevivência do “mais apto”). Mas não só isso, as propriedades emergentes, citadas por Stariolo, também estão presentes: a evolução cria e modifica seus próprios padrões não-lineares e portanto é auto organizada; ela ocorre em múltiplas escalas, sejam elas temporais ou espaciais; e apresentam grande complexidade, ou seja existem muitos equilíbrios (ou espécies) possíveis – é bem provável que outras combinações de espécies estariam presentes no mundo hoje, caso alguma coisa tivesse acontecido diferente no passado. Entender em detalhe quais as relações e as regras da evolução têm sido o desafio dos biólogos (e físicos!) nos últimos anos.

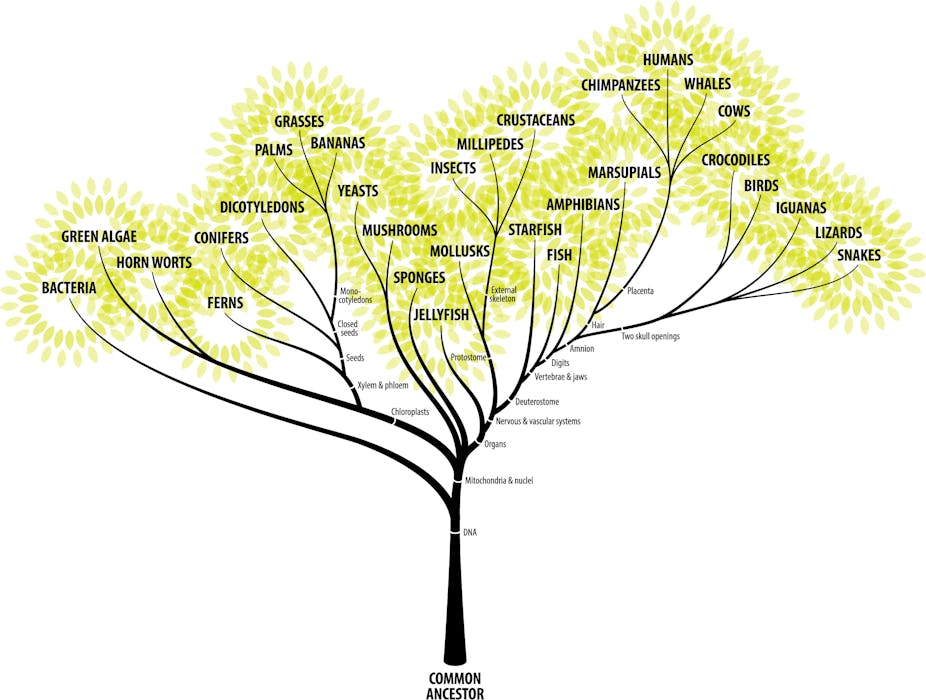
Árvore da vida. A evolução não é um processo linear como normalmente imaginado pelo senso comum. Trata-se de um exemplo de sistema complexo com diversos agentes atuantes. (Fonte: ZernLiew)

O problema do caixeiro viajante

Um dos exemplos clássicos que o professor trouxe foi o conhecido “Problema do Caixeiro Viajante”. O problema é, conceitualmente, simples: qual a menor rota possível para o caixeiro passar (somente uma vez) por todas as cidades de um determinado grupo de cidades e voltar para o ponto inicial.

A princípio, pode parecer uma pergunta boba ou sem sentido, mas, na verdade, soluções desse problema têm aplicações diretas e indiretas em diversas áreas, desde planejamento e logística no transporte de mercadorias, até produção de microchips, sequenciamento de DNA e astronomia.

A origem do problema é relativamente incerta: existem registros de que esse problema tenha sido proposto no século 19, mas foi considerado matematicamente apenas na década de 30. Já nessa época, Karl Menger, um dos matemáticos que teria estudado o problema, concluiu a necessidade de um algoritmo potente para resolvê-lo e postulou que a solução “óbvia”, que comumente vem primeiro à mente, geralmente não é a resposta certa. Ele se referia a regra “do ponto mais próximo” em que, partindo de uma cidade, a rota deveria seguir sempre para a cidade seguinte mais próxima. Embora essa solução pareça razoável, nem sempre a soma total dos deslocamentos será a menor possível – e portanto, não responde ao problema original.

Stariolo mostrou um vídeo durante sua apresentação, e vamos fazer o mesmo aqui. Basicamente, o vídeo apresenta quatro respostas usando, cada um, uma abordagem diferente, para o problema: qual a menor rota possível para ligar as 200 cidades do vídeo.

O primeiro método é selecionar aleatoriamente as cidades até que todas tenham sido visitadas. Ou seja, é “deixar a vida te levar”. Essa abordagem que pode funcionar muito bem quando você está viajando a lazer e resultou no percurso de 327452.4 km percorrido entre as cidades.

O segundo método é o de escolher sempre a cidade mais próxima – a solução “óbvia” que vêm à mente, como falado nos parágrafos anteriores. Provavelmente seria a solução que um turista um pouco mais preparado teria escolhido. No caso do vídeo, a distância total percorrida seria 36226.2km.

A terceira abordagem utiliza o método inicial, criando uma rede aleatória, mas o otimiza, sempre selecionando 2 pontas para trocar. A não ser que seu problema a resolver seja trivial, escolher quais pontas trocar é complicado. Assim, a solução é que o algoritmo faça trocas aleatórias até que encontre a menor rota. O problema dessa abordagem é que, por conta do caminho inicial escolhido, o algoritmo empaca numa solução que não é a melhor possível – e pode ser um “mínimo local”, que não necessariamente é o mínimo global do seu sistema. Nesse caso, o viajante teria percorrido 31887.0 km

Para entender o mínimo local, imagine um vale com montanhas bem altas, mas que também tem montanhas menores ao redor. Pode ser que, procurando o ponto mais baixo entre as montanhas, você caia num vale entre uma montanha grande e uma pequena, mas não necessariamente no ponto mais baixo de todas as montanhas ali (Fonte:i2tutorials)

Como melhorar isso? Utilizando uma técnica probabilística chamada recozimento simulado (simulated annealing), que tem suas origens na termodinâmica.

Para resolver o problema do caixeiro viajante, usar o recozimento simulado permite aceitar probabilisticamente soluções ruins no início da busca. Quanto tempo a busca pelo menor caminho vai durar é medida de acordo com uma temperatura hipotética para o sistema. No início da busca, a temperatura é alta e a chance de aceitar resultados ruins é maior. Com a diminuição da temperatura, também diminui a probabilidade de que a resposta obtida não seja a ideal. No caso do vídeo, o caminho ideal entre as 200 cidades é encontrado quanto a “temperatura do sistema” é 0.4, encontrando uma solução de 30944.3 km.

Recapitulando… a abordagem completamente aleatória percorreria 327 mil quilômetros; ligando sempre o ponto mais próximo, a segunda, 36,2 mil km; a terceira, usando otimização, 31,9 mil km; e, por fim, a quarta, que usa otimização e recozimento simulado, 31,0 mil km.

Claramente, o método do turista “deixa a vida me levar” é o mais longo de todos – e às vezes esse pode até ser o objetivo do turista. Mas quando falamos do transporte de cargas e da logística de mercadorias, é interessante para as empresas gastar o mínimo possível, ou seja, tomar a menor rota possível.

A diferença mais expressiva é entre o ‘viajar sempre para a cidade mais próxima’ e os métodos probabilísticos mais robustos. Considere um caminhão viajando constantemente a 80km/h e cujo desempenho seja 29 litros/100km. A alternativa 2, indo sempre à cidade mais próxima, gastaria 10500 litros ao longo de 453 horas (ou seja, 18.9 dias corridos). Usando a melhor das rotas calculadas, seriam utilizados 1530 litros de combustível a menos, e 2,8 dias seriam economizados na conta do motorista. Se você imaginar grandes companhias com milhares de caminhoneiros transportando mercadoria todos os dias, isso faz uma baita diferença!

Mas o que física tem a ver com isso tudo?

Primeiramente, princípios de física são utilizados para entender como funciona a natureza. Sistemas complexos ocorrem nas mais diversas escalas e nos mais diversos locais na natureza, então é esperado que a física poderia ser usada para estudá-los. Além disso, a física já tem um conceito que está relacionado o grau de desordem de um sistema – a entropia – e uma área de estudo que se propõe a estudá-la: a termodinâmica.

A termodinâmica pode ser estudada tanto pela mecânica clássica, com as leis de Newton, quanto pela mecânica quântica, com todas as estranhezas intrínsecas ao mundo do muito pequeno. Mas, quando tratamos de uma quantidade muito grande de objetos a serem estudados – moléculas, átomos, elétrons -, é necessário usar a física estatística. A ideia é aliar probabilidade e estatística para caracterizar o comportamento médio (ou probabilístico) de sistemas microscópicos onde existam muitos elementos interagindo. Stariolo ainda comenta que a física estatística é, grosso modo, a termodinâmica na escala microscópica.

Vale lembrar que nem todo sistema estudado com física estatística é um sistema complexo, por conta das outras características intrínsecas deles, como já mencionado neste texto. Um sistema complicado de entender não necessariamente é um sistema complexo! Mesmo assim, a física estatística é uma ferramenta para o estudo dos sistemas complexos, e rompe as barreiras do mundo micro – com ela é possível estudar desde os átomos e moléculas, até as redes sociais e a economia mundial.

O Papos de Física é um evento mensal de divulgação científica promovido pelo ICTP-SAIFR no Tubaína Bar (R. Haddock Lobo, 74). Todo mês, levamos pesquisadores para conversar com o público leigo sobre assuntos intrigantes da física, em palestras descontraídas e informais. Fique ligado para os eventos de 2020 no nosso instagram e na página!

Para saber mais sobre sistemas complexos e a física por trás deles:

SAIFR Divulga! – A Mecânica Estatística só se aplica a fenômenos físicos?

http://www.cbpf.br/~desafios/media/livro/Sistema_complexos.pdf

Entre os dias 2 e 14 de julho, o ICTP-SAIFR e o IFT-UNESP, em São Paulo, sediaram uma Escola de Modelos Integráveis voltada para especialistas de várias áreas da física. 

Organizadores, participantes e palestrantes da Escola de Modelos Integráveis. Na segunda fileira, à direita, o organizador Pedro Vieira, do ICTP-SAIFR-IFT-UNESP & Perimeter Institute, Canadá.

A Escola de Modelos Integráveis aconteceu no campus do IFT-UNESP, na Barra Funda, com um programa que integrou e atualizou jovens pesquisadores e especialistas das áreas de mecânica estatística, matemática, matéria condensada, teorias de calibre e teoria de cordas sobre a ferramenta da integrabilidade – usada para resolver exatamente sistemas como, por exemplo, cadeias de spin – mecânica estatística -; modelos de vértice – que se expandiram do contexto da física nuclear para a teoria de cordas -; e ads/cft, correspondência entre teorias definidas em espaços anti-deSitter e de campos conformes.

O evento foi o terceiro de uma série de escolas coordenadas na área de Modelos Integráveis. A primeira foi realizada pelo NORDITA, Nordic Institute for Theoretical Physics, na Suécia, entre 14 de maio e 8 de junho, e a segunda aconteceu no IIP, International Institute of Physics, em Natal, Brasil, de 18 a 29 de junho. Pesquisadores sediados na Suécia, EUA e Brasil – Konstantin Zarembo (NORDITA, Suécia), Shota Komatsu (Princeton, EUA) e Valdimir Korepin (State University of New York, EUA) e Márcio Martins (UFSCar, Brasil) – apresentaram as novidades da áea de modelos integráveis para osparticipantes. Além de assitir aos cursos,os participantes também apresentaram seus trabalhos, na segunda semana do evento. O comitê organizador foi fomado por pesquisadores sediados nos EUA, Vladimir Korepin (State University of New York at Stony Brook), na França, Didina Serban (IPhT-Saclay) e no Brasil, Giuliano Ribeiro (UFSCar) e Pedro Vieira (ICTP-SAIFR/IFT-UNESP & Perimeter Institute, Canadá).